TL;DR#
flox>=0.9 now automatically optimizes GroupBy reductions with dask arrays to reduce memory usage and increase parallelism! Here I describe how. To opt in, simply set method=None if you were setting it explicitly previously.
What is flox?#
flox implements grouped reductions for chunked array types like cubed and dask using tree reductions.
Tree reductions (example) are a parallel-friendly way of computing common reduction operations like sum, mean etc.
Briefly, one computes the reduction for a subset of the array N chunks at a time in parallel, then combines those results together again N chunks at a time, until we have the final result.
Without flox, Xarray effectively shuffles — sorts the data to extract all values in a single group — and then runs the reduction group-by-group.
Depending on data layout or "chunking" this shuffle can be quite expensive.
Here's a schematic of an array with 5 chunks arranged vertically, and each chunk has 10 elements each of which are colored by group.
With flox installed, Xarray instead uses its parallel-friendly tree reduction.
In many cases, this is a massive improvement.
Notice how much cleaner the graph is in this image:
See our previous blog post or the docs for more.
Tree reductions can be catastrophically bad#
Consider ds.groupby("time.year").mean(), or the equivalent ds.resample(time="Y").mean() for a 100 year long dataset of monthly averages with chunk size of 1 (or 4) along the time dimension.
This is a fairly common format for climate model output.
The small chunk size along time is offset by much larger chunk sizes along the other dimensions — commonly horizontal space (x, y or latitude, longitude).
A naive tree reduction would accumulate all averaged values into a single output chunk of size 100 — one value per year for 100 years. Depending on the chunking of the input dataset, this may overload the final worker's memory and fail catastrophically. More importantly, there is a lot of wasteful communication — computing on the last year of data is completely independent of computing on the first year of the data, and there is no reason the results for the two years need to reside in the same output chunk. This issue does not arise for regular reductions where the final result depends on the values in all chunks, and all data along the reduced axes are reduced down to one final value.
Avoiding catastrophe#
Thus flox quickly grew two new modes of computing the groupby reduction.
Two key realizations influenced that development:
- Array workloads frequently group by a relatively small in-memory array. Quite frequently those arrays have patterns to their values e.g.
"time.month"is exactly periodic,"time.dayofyear"is approximately periodic (depending on calendar),"time.year"is commonly a monotonic increasing array. - Chunk sizes (or "partition sizes") for arrays can be quite small along the core-dimension of an operation. So a grouped reduction applied blockwise need not reduce the data by much (or any!) at all. This is an important difference between arrays and dataframes!
These two properties are particularly relevant for "climatology" calculations (e.g. groupby("time.month").mean()) — a common Xarray workload in the Earth Sciences.
First, method="blockwise" which applies the grouped-reduction in a blockwise fashion.
This is great for resample(time="Y").mean() where we group by "time.year", which is a monotonic increasing array.
With an appropriate (and usually quite cheap) rechunking, the problem is embarrassingly parallel.
Second, method="cohorts" which is a bit more subtle.
Consider groupby("time.month") for the monthly mean dataset i.e. grouping by an exactly periodic array.
When the chunk size along the core dimension "time" is a divisor of the period; so either 1, 2, 3, 4, or 6 in this case; groups tend to occur in cohorts ("groups of groups").
For example, with a chunk size of 4, monthly mean input data for the "cohort" Jan/Feb/Mar/Apr are always in the same chunk, and totally separate from any of the other months.
Here is a schematic illustration where each month is represented by a different shade of red and a single chunk contains 4 months:
 This means that we can run the tree reduction for each cohort (three cohorts in total:
This means that we can run the tree reduction for each cohort (three cohorts in total: JFMA | MJJA | SOND) independently and expose more parallelism.
Doing so can significantly reduce memory required for the computation.
Finally, if there isn't much separation of groups into cohorts, like when groups are randomly distributed across chunks, then it's hard to do better than the standard method="map-reduce".
Choosing a strategy is hard, and harder to teach.#
These strategies are great, but the downside is that some sophistication is required to apply them. Worse, they are hard to explain conceptually! I've tried! (example 1, example 2).
What we need is to choose the appropriate strategy automatically.
Demo#
Here's a quick demo of computing monthly mean climatologies with the National Water Model.
For this input dataset, chunked so that approximately a month of data is in a single chunk,
we run
1mean_mapreduce = ds.groupby("time.month").mean(method="map-reduce") 2mean_cohorts = ds.groupby("time.month").mean() # this is auto-detected! 3
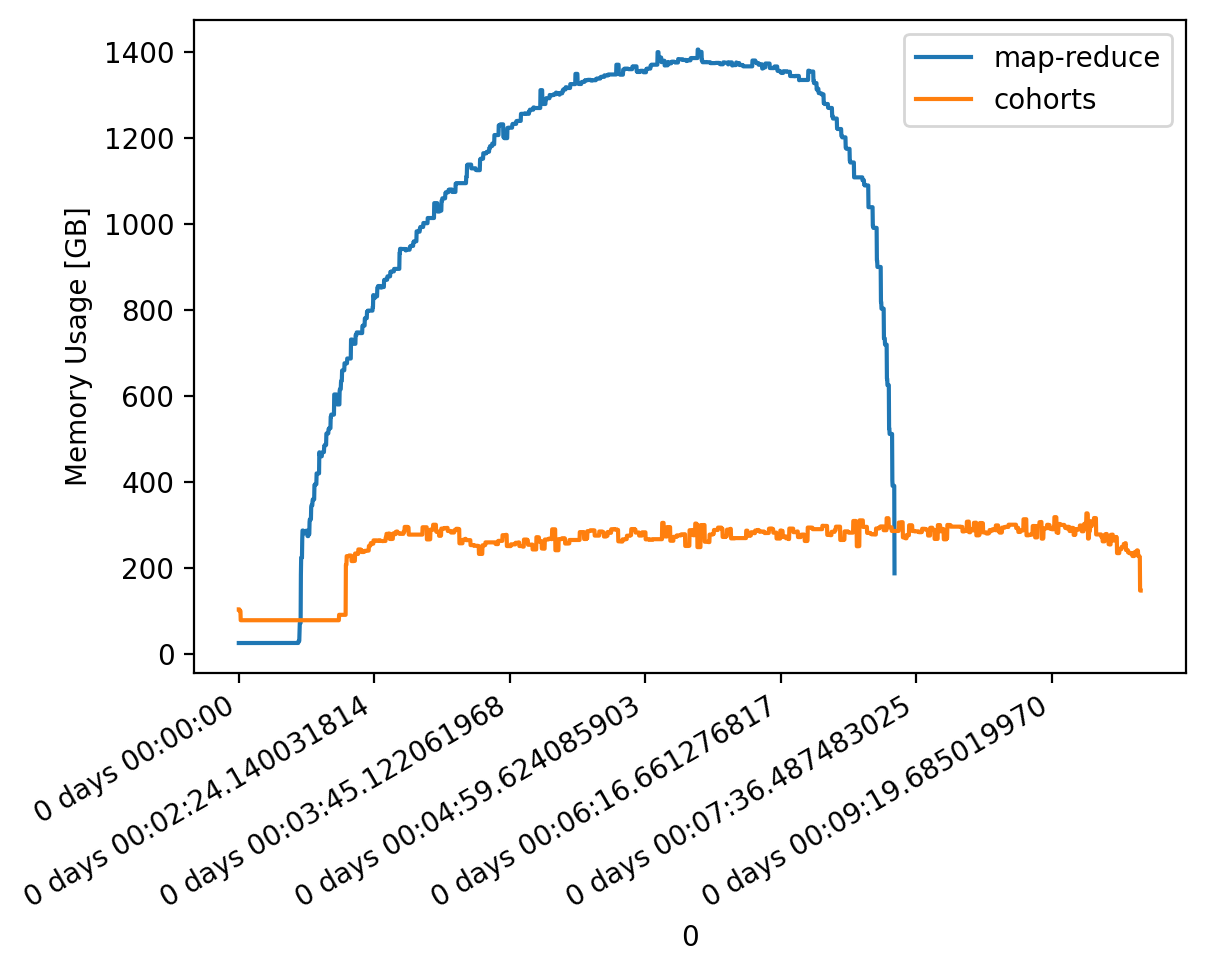
Using the algorithm described below, flox will automatically set
method="cohorts" for this dataset unless specified, yielding a 5X decrease in
memory need, and 2X longer in time
Problem statement#
Fundamentally, we know:
- the data layout or chunking.
- the array we are grouping by, and can detect possible patterns in that array.
We want to find all sets of groups that occupy similar sets of chunks.
For groups A,B,C,D that occupy the following chunks (chunk 0 is the first chunk along the core-dimension or the axis of reduction)
A: [0, 1, 2] B: [1, 2, 3, 4] C: [5, 6, 7, 8] D: [8] X: [0, 4]
We want to detect the cohorts {A,B,X} and {C, D} with the following chunks.
[A, B, X]: [0, 1, 2, 3, 4] [C, D]: [5, 6, 7, 8]
Importantly, we do not want to be dependent on detecting exact patterns, and prefer approximate solutions and heuristics.
The solution#
After a fun exploration involving such fun ideas as locality-sensitive hashing, and all-pairs set similarity search, I settled on the following algorithm.
I use set containment, or a "normalized intersection", to determine the similarity between the sets of chunks occupied by two different groups (Q and X).
C = |Q ∩ X| / |Q| ≤ 1; (∩ is set intersection)
Unlike Jaccard similarity, containment isn't skewed when one of the sets is much larger than the other.
The steps are as follows:
- First determine which labels are present in each chunk. The distribution of labels across chunks
is represented internally as a 2D boolean sparse array
S[chunks, labels].S[i, j] = 1when labeljis present in chunki. - Now invert
Sto compute an initial set of cohorts whose groups are in the same exact chunks (this is another groupby!). Later we will want to merge together the detected cohorts when they occupy approximately the same chunks, using the containment metric. - Now we can quickly determine a number of special cases and exit early:
- Use
"blockwise"when every group is contained to one block each. - Use
"cohorts"when- every chunk only has a single group, but that group might extend across multiple chunks; and
- existing cohorts don't overlap at all.
- and more
- Use
If we haven't exited yet, then we want to merge together any detected cohorts that substantially overlap with each other using the containment metric.
- For that we first quickly compute containment for all groups
iagainst all other groupsjasC = S.T @ S / number_chunks_per_group. - To choose between
"map-reduce"and"cohorts", we need a summary measure of the degree to which the labels overlap with each other. We use sparsity --- the number of non-zero elements inCdivided by the number of elements inC,C.nnz/C.size. When sparsity is relatively high, we use"map-reduce", otherwise we use"cohorts". - If the sparsity is low enough, we merge together similar cohorts using a for-loop.
For more detail see the docs or the code. Suggestions and improvements are very welcome!
Here is containment C[i, j] for a range of chunk sizes from 1 to 12 for computing groupby("time.month") of a monthly mean dataset.
These panels are colored so that light yellow is C=0, and dark purple is C=1.
C[i,j] = 1 when the chunks occupied by group i perfectly overlaps with those occupied by group j (so the diagonal elements
are always 1).
Since there are 12 groups, C is a 12x12 matrix.
The title on each image is (chunk size, sparsity).

When the chunksize is a divisor of the period 12, C is a block diagonal matrix.
When the chunksize is not a divisor of the period 12, C is much less sparse in comparison.
Given the above C, flox will choose "cohorts" for chunk sizes (1, 2, 3, 4, 6), and "map-reduce" for the rest.
Cool, isn't it?!
Importantly this inference is fast — ~250ms for the US county GroupBy problem in our previous post where approximately 3000 groups are distributed over 2500 chunks; and ~1.25s for grouping by US watersheds ~87000 groups across 640 chunks.
What's next?#
flox' ability to do cleanly infer an optimal strategy relies entirely on the input chunking making such optimization possible. This is a big knob. A brand new Xarray feature does make such rechunking a lot easier for time grouping in particular:
1from xarray.groupers import TimeResampler 2 3rechunked = ds.chunk(time=TimeResampler("YE")) 4
will rechunk so that a year of data is in a single chunk. Even so, it would be nice to automatically rechunk to minimize number of cohorts detected, or to a perfectly blockwise application when that's cheap.
A challenge here is that we have lost context when moving from Xarray to flox.
The string "time.month" tells Xarray that I am grouping a perfectly periodic array with period 12; similarly
the string "time.dayofyear" tells Xarray that I am grouping by a (quasi-)periodic array with period 365, and that group 366 may occur occasionally (depending on calendar).
But Xarray passes flox an array of integer group labels [1, 2, 3, 4, 5, ..., 1, 2, 3, 4, 5].
It's hard to infer the context from that!
Though one approach might frame the problem as: what rechunking would transform C to a block diagonal matrix.
Get in touch if you have ideas for how to do this inference.
One way to preserve context may be be to have Xarray's new Grouper objects report "preferred chunks" for a particular grouping.
This would allow a downstream system like flox or cubed or dask-expr to take this in to account later (or even earlier!) in the pipeline.
That is an experiment for another day.